Kuboyama Laboratory

Research

My research areas are in data mining and machine learning. I am primarily working on the following research themes:

Similarity Measure Design for Discrete Data Structures

I design similarity measures for discrete data structures more complex than strings, such as tree structures, ordered structures, and graph structures. I investigate their theoretical properties and apply the results to data mining and machine learning.

Similarity and Distance Design

Tree structures play an important role in various algorithms and are used to represent syntactic trees, phylogenetic trees, and glycan structures in biology.

When two tree structures are given, how similar are these two structures? The metric (similarity or distance) to evaluate this degree is not unique.

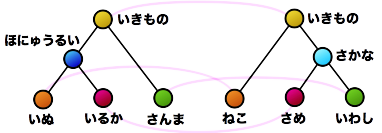
tree mapping
Mapping between two trees (result of edit distance calculation)
Tree edit distance by Tai

The coarsest evaluation method is to ask whether the two structures are perfectly identical (isomorphism testing). Efficient algorithms are known for tree isomorphism testing. However, the problem of evaluating how similar the structures are while tolerating some mismatches is not so simple because:

The widely used edit distance is defined by the minimum cost of edit operations to transform one structure into another. In this research, I organized various tree edit distance algorithms and similarity concepts that had been developed without clear criteria, clarifying their interrelationships.

Alignment of two trees

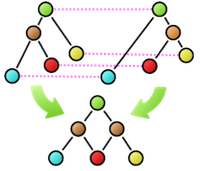
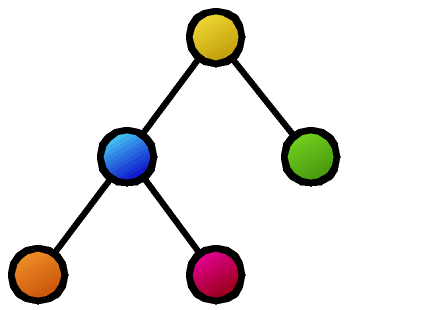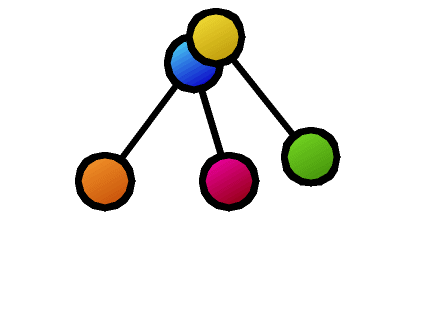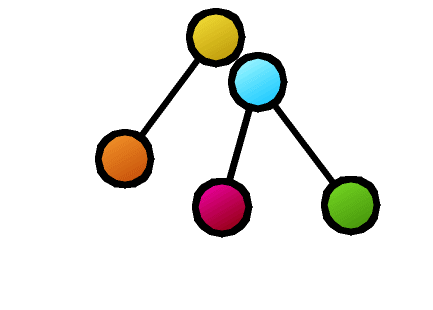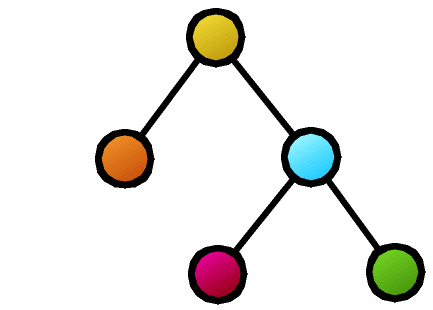
Furthermore, many basic properties related to tree comparison are surprisingly unknown. For example, as shown in the figure, suppose that as a result of calculating the similarity between two trees, the nodes connected by dashed lines correspond to each other. Is it possible to create a new composite tree (supertree) by overlapping these corresponding nodes while maintaining the hierarchical relationships of each tree? In this example, the red nodes become confluent points, making it impossible to maintain the tree structure. The necessary and sufficient conditions for taking node correspondences such that the composite becomes a tree structure after composition were first clarified by our research.

I approach the design of similarity and distance measures from mainly two perspectives:

Optimization Problems
Design similarity/distance measures as maximization of common parts (maximum common subtree problem) or minimization of mismatched parts (tree edit distance problem). The advantage is that constructively, which parts are similar can be understood from the calculation result (represented as lines connecting the two tree structures in the figure).
Enumeration Problems
Counting of common substructures. The advantages of calculating similarity/distance as an enumeration problem are that local similarities can be captured, that constructive calculation is not necessarily required, and that it can be immediately applied to classification learning of tree structures (tree kernel design in machine learning).

These fundamental research results have been applied to classification learning of cancer-derived glycan structures and analysis of temporal community hierarchical structures.

Main Collaborative Research

Development of Fast Feature Selection Algorithms

Fast feature selection algorithm

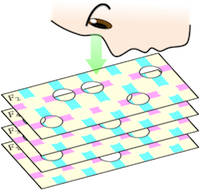
Feature selection is the problem of extracting only the necessary attributes from data with numerous attributes for a specific purpose. It is an important fundamental problem in data mining and machine learning.

In this research, I focus on the feature selection problem for categorical data, which includes interesting subproblems connecting discrete and continuous domains. I work on analyzing the theoretical properties of CWC, which is one of the most high-performing existing algorithms, improving the algorithm, and applying it. CWC formulates the feature selection problem as a kind of set covering problem and extracts features using a greedy method (the figure shows an image of the algorithm).

Despite using a very simple evaluation metric to decide whether to keep features, CWC has been shown experimentally to perform very well on various benchmarks. Currently, I am conducting analysis to theoretically support this high performance.

I am also applying this algorithm not only as a preprocessing step for machine learning but also for rapid topic word extraction from massive documents.

Developed Software

Main Collaborative Research

Analysis of Public Works Bidding Data

Community structure formed by bidders

The bid rate is widely known as a criterion for judging appropriate competitive bidding versus bid-rigging. However, solving a regression problem with the bid rate as the objective variable does not necessarily allow for analyzing the appropriateness of competitive bidding.

In this research, I focus on the connections between companies participating in bidding and analyze the temporal changes in their structure and changes in company communities. The figure visualizes the connections between bidding companies of a local government as a network.

Currently, I am developing new element technologies for bidding data analysis by extracting and analyzing the relationships hidden in massive bidding data. In particular, I am researching time-series network community extraction methods to discover groups of companies that participate in the same bids exclusively.

Main Collaborative Research

User Behavior Estimation from Computer Logs

I am estimating user behavior using computer log information, particularly active window transition data.

First, assuming that window transitions are generated by underlying tasks, I segment the logs using hidden Markov models. Using these abstracted task units, I create state transition diagrams for each user. Viewing the state transition diagrams as graph structures, I cluster users with similar work patterns using graph kernels and kernel principal component analysis. Though the idea is simple, it yields interpretable results that correspond to actual business operations.

I am also conducting analyses to determine work attendance status by extracting statistical features of window switching.

Genetic Mutation Analysis of Influenza Viruses

Embedding of genetic distances between influenza viruses

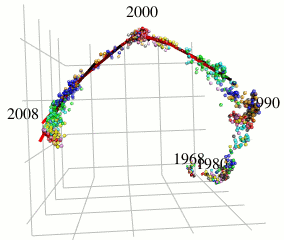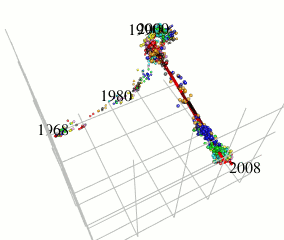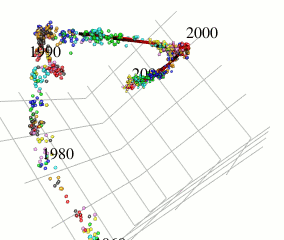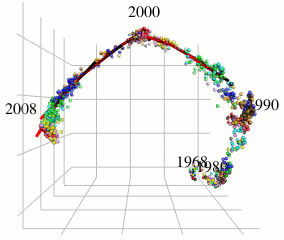
In this research, I focus on type A influenza viruses that cause global epidemics, aiming to construct a continuous mutation model of antigens from amino acid sequence data. I use an approach different from existing research on mutation prediction and co-mutation pattern extraction by Professor Ito of the Research Center for Zoonosis Control, Hokkaido University.

Existing research predicts mutations by observing changes in the hemagglutinin gene’s amino acid sequence within the Hamming distance space. In contrast, this research extracts only the components of influenza virus evolution direction using locally sparse principal component analysis by embedding the amino acid symbol space into Euclidean distance space (with low distortion) while preserving the properties of the Hamming distance space (see figure). This method has improved the prediction performance of existing methods.

Main Collaborative Research

Time-Series Topic Extraction from Social Media

I am attempting to extract the evolution of user needs from time-series data such as Twitter, blogs, and review comments on shopping sites. For element technologies, I use various methods including topic extraction methods from the natural language understanding field, hierarchical community extraction methods for networks, and methods combining tree edit distance.

Main Collaborative Research